Fourier Series
Any curve is a collection of 2 dimensional points on a surface. It is imperative that 2 dimensional information can be gracefully expressed in mathematics using complex numbers. This can also be thought of a signal which is complexed valued (discrete or continuous).
We already know, a signal can be expressed of some linear combinations of shifted delta functions and if our system is linear this notion of linear combination can be exploited for ease of operation. However, in Fourier Series, we will express the signal using something else. We will break down a signal into Rotating Circles.
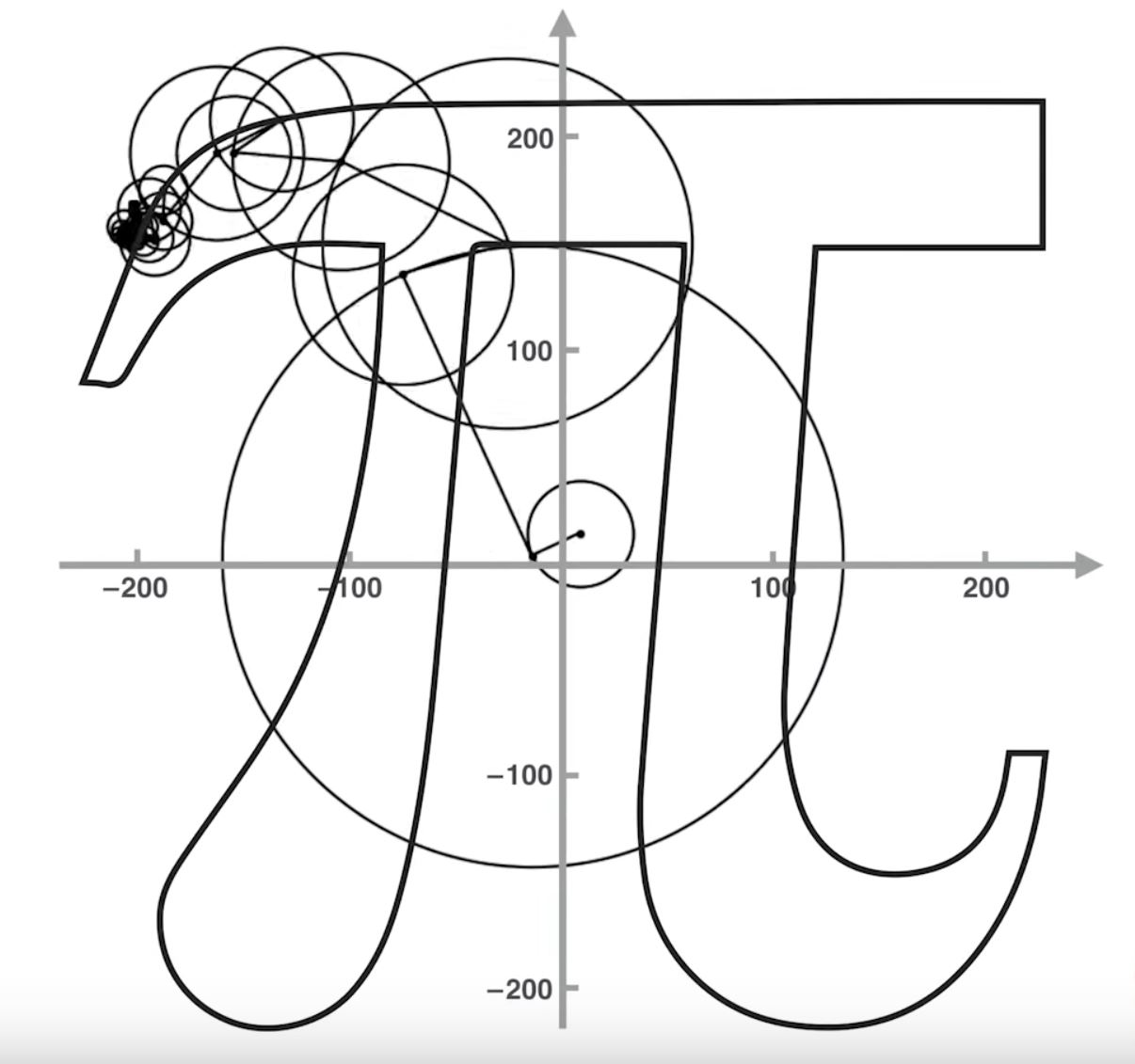
Using enough rotating circles we can draw almost anything by setting three basic information of these circle.
- Speed of rotation or frequency $\omega$
- Initial configuration of the arrow head or phase $\phi$
- Size of the arrows or the amplitude $A$
But why would we want to use this kind of dissection of a signal to all these rotating circles? The applications are numerous. From solving physics problem to engineering communication system, the concept is super useful.
For most of the physical system, the differential equations behave very nicely with exponentials. This is because no matter how many times you differentiate an exponential, it will be a scaled version of it’s previous state.
\[\frac{d^n}{dx^n} e^Ax = A^n e^{Ax}\]Thus, it is very obvious the whole system will behave too nicely if the inputs to the system is exponential. In the video of Grant Sanderson, he mentioned the heat equation. This is also very similar in case of something like Electro-magnetic system or even physical spring damper systems.
One other nice thing about and exponential is that the exponent can be complex or imaginary number. That directly translates to rotation in the complex plane.
\[e^{j \theta} = cos \theta + j sin \theta\]In this equation, if we set $\theta$ to be a function of time, we have a rotating complex number!
\[e^{j \omega t} = cos (\omega t) + j sin (\omega t)\]Now, we just have to change the amplitude and the phase. We can easily do so by multiplying the whole thing via another complex number with $A$ magnitude and $\phi$ phase.
\[A \angle \phi \; e^{j \omega t }\]Now, we have complete control over one rotating arrow. We can easily build any signal by superimposing many of this rotating circles one after another.
\[A_1 \angle \phi_1 \; e^{j \omega_1 t} + A_2 \angle \phi_2 \; e^{j \omega_2 t} + A_3 \angle \phi_3 \; e^{j \omega_3 t} + ...\]This whole mathematical expression should be now equivalent to many arrows superimposed on each other with amplitude, phase and frequency dictated by us. By controlling these knobs and dials of the system we can generated any signal, if we have infinite terms. With finite terms, we can almost approximate any shape with very minimal truncation error. This series of complex terms is called the Fourier Series Approximation of the whole signal.
\[\sum_{k=0}^{\infty} A_i \angle \phi_i \; e^{j \omega k t}\]